목차
728x90
그래프를 탐색하는 방법 2 - BFS(Breadth-First Search) : 인접행렬-O(V^2), 인접리스트- O(V + E)
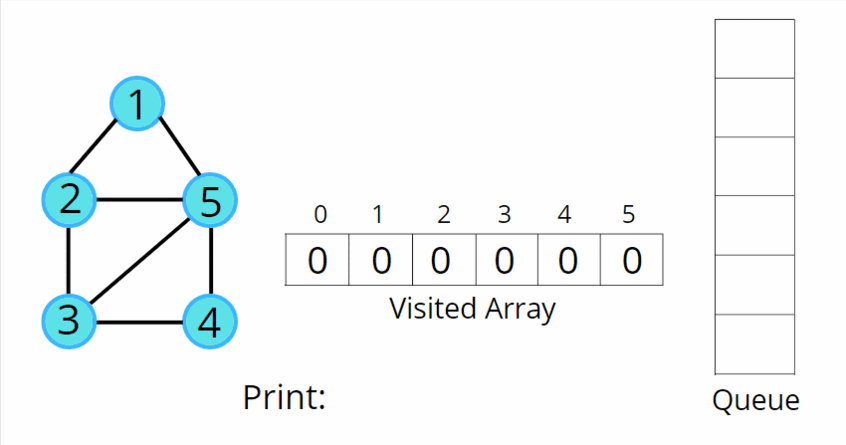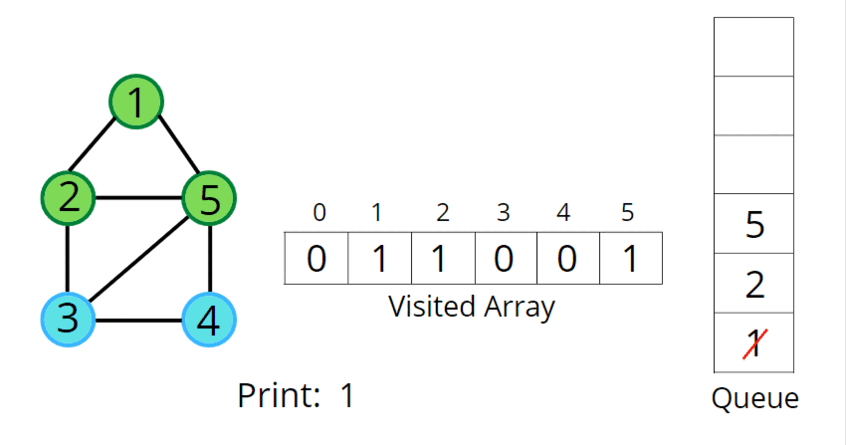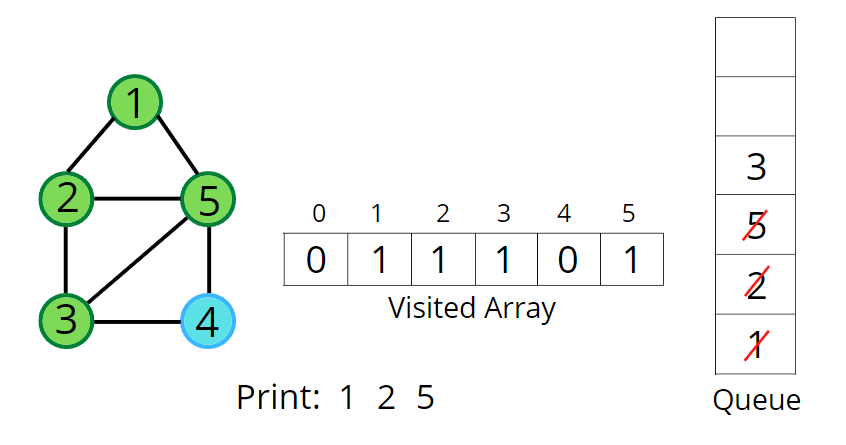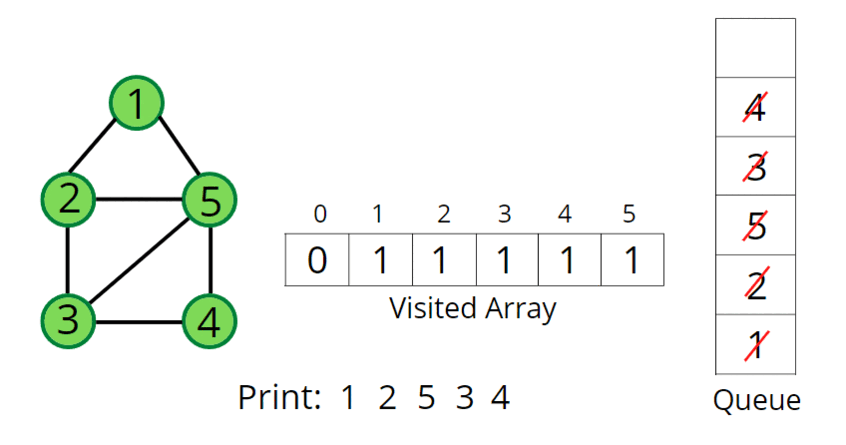
BFS_인접행렬 코드
/*
https://www.acmicpc.net/problem/1260
4 5 1
1 2
1 3
1 4
2 4
3 4
*/
package ureca;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class BFS_인접행렬{
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
StringBuilder sb = new StringBuilder(100);
//입력 받음
int V=scanner.nextInt(); // 정점의 개수
int E=scanner.nextInt(); // 간선의 개수
int startNo = scanner.nextInt(); // 탐색 시작할 정점 번호
int[][] adjMatrix = new int[V + 1][V + 1]; // 간선 정보를 넣을 배열, 시작정점이 1이라면 0번행열은 쓰지 않는게 좋음
boolean []isSelected=new boolean[V+1];
// 간선 정보를 입력받아 인접 행렬을 구성
for (int i = 0; i < E; i++) {
int from = scanner.nextInt();
int to = scanner.nextInt();
adjMatrix[from][to] = adjMatrix[to][from] = 1; // 무방향 그래프이므로
}
// BFS 탐색 시작
Queue<Integer> queue = new LinkedList<>(); // 큐 생성
queue.offer(startNo); // 시작 정점 큐에 추가
isSelected[startNo] = true; // 시작 정점 방문 처리
while (!queue.isEmpty()) {
int cur = queue.poll(); // 큐에서 정점 꺼내기
sb.append(cur).append(" "); // 결과 문자열에 추가
// 현재 정점에서 갈 수 있는 모든 후보지 탐색
for (int i = 1; i <= V; i++) {
if (!isSelected[i] && adjMatrix[cur][i] != 0) { // 방문하지 않았고, 연결된 정점인 경우
queue.offer(i); // 큐에 추가
isSelected[i] = true; // 방문 처리
}
}
}
sb.append("\n");
// 결과 출력
System.out.print(sb.toString());
scanner.close();
}
}BFS_인접리스트 코드
import java.util.*;
public class 백준_1260_BFS_인접리스트 {
static List<List<Integer>> list=new ArrayList();
static boolean[] isSelected;
static StringBuilder sb=new StringBuilder();
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
isSelected=new boolean[n+1];
for (int i = 1; i <= n+1; i++) {
list.add(new ArrayList());
}
int m=sc.nextInt();
int startNode=sc.nextInt();
for(int i=0;i<m;i++) {
int u=sc.nextInt();
int v=sc.nextInt();
list.get(u).add(v);
list.get(v).add(u);
}
Queue<Integer> q=new LinkedList();
q.offer(startNode);
isSelected[startNode]=true;
while(!q.isEmpty()) {
int curNode=q.poll();
sb.append(curNode).append(" ");
for (int i :list.get(curNode)) {
if(!isSelected[i]) {
q.offer(i);
isSelected[i]=true;
}
}
}
System.out.println(sb);
}
}(6) 그래프 응용 - 최단경로
a)가중치가 없는 그래프에서 정점간의 최단 경로를 찾는 방법은 BFS가 최고 (ex. 바둑판 미로 찾기)
i)경로를 추적하기 위해 parent의 정보를 저장할 배열을 사용하는 경우
/*
### 문제: 최단 경로 찾기
**문제 설명**
주어진 무방향 그래프에서 두 노드 간의 최단 경로를 찾는 프로그램을 작성하시오. 그래프는 N개의 노드와 M개의 간선으로 구성되어 있으며, 각 간선은 두 노드를 연결합니다. 시작 노드와 목표 노드가 주어질 때, 이 두 노드 간의 최단 경로를 출력하시오.
**입력**
- 첫째 줄에 두 개의 정수 N(1 ≤ N ≤ 1000)과 M(1 ≤ M ≤ 10000)이 주어진다. N은 노드의 개수, M은 간선의 개수이다.
- 다음 M개의 줄에는 간선 정보가 주어진다. 각 줄은 두 개의 정수 u와 v(1 ≤ u, v ≤ N)를 포함하며, 이는 노드 u와 노드 v가 간선으로 연결되어 있음을 의미한다.
- 마지막 줄에는 시작 노드 S와 목표 노드 G가 주어진다.
**출력**
- 시작 노드 S에서 목표 노드 G까지의 최단 경로를 출력한다. 경로는 노드 번호로 구성되어야 하며, 경로가 존재하지 않는 경우 `-1`을 출력한다.
**입력**
5 5
1 2
1 3
2 4
3 4
4 5
1 5
**출력**
1 2 4 5
*/
import java.util.*;
public class BFS_최단경로 {
static StringBuilder sb = new StringBuilder(); // 경로를 저장할 StringBuilder
static List<Integer> path = new ArrayList<>(); // 최단 경로를 저장할 리스트
static boolean found = false; // 경로가 발견되었는지 여부를 저장하는 변수
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 노드의 수 N과 간선의 수 M을 입력받음
int N = sc.nextInt(); // 노드의 수
int M = sc.nextInt(); // 간선의 수
// 인접 리스트를 생성
List<List<Integer>> list = new ArrayList<>();
for (int i = 0; i <= N; i++) {
list.add(new ArrayList<>()); // 각 노드에 대한 리스트 초기화
}
// 간선 정보를 입력받아 인접 리스트에 추가
for (int i = 0; i < M; i++) {
int from = sc.nextInt(); // 간선의 시작 노드
int to = sc.nextInt(); // 간선의 끝 노드
list.get(from).add(to); // 양방향 그래프이므로 양쪽에 추가
list.get(to).add(from);
}
// 시작 노드 S와 목표 노드 G를 입력받음
int start = sc.nextInt();
int goal = sc.nextInt();
// 방문 여부를 체크할 배열
boolean[] visited = new boolean[N + 1];
// 부모 노드를 저장할 배열 (경로 추적을 위해 사용)
int[] parent = new int[N + 1];
// BFS를 위한 큐 초기화
Queue<Integer> q = new LinkedList<>();
q.offer(start); // 시작 노드를 큐에 추가
visited[start] = true; // 시작 노드를 방문 처리
parent[start] = -1; // 시작 노드의 부모는 없음
// BFS 탐색 시작
while (!q.isEmpty()) {
int cur = q.poll(); // 큐에서 현재 노드를 꺼냄
// 목표 노드에 도달한 경우
if (cur == goal) {
found = true; // 경로 발견
break; // 탐색 종료
}
// 현재 노드와 연결된 모든 노드를 탐색
for (int i : list.get(cur)) {
if (!visited[i]) { // 방문하지 않은 노드인 경우
q.offer(i); // 큐에 추가
visited[i] = true; // 방문 처리
parent[i] = cur; // 현재 노드를 부모로 설정
}
}
}
if (found) {// 경로가 발견된 경우
// 목표 노드에서 시작 노드까지 부모를 통해 경로를 추적
for (int at = goal; at != -1; at = parent[at]) {
sb.append(at).append(" "); // 결과에 추가
}
System.out.println(sb.reverse().toString().trim());
}else{
System.out.println(-1);
}
}
}728x90
'💡 URECA > 🗒️ 스터디 노트' 카테고리의 다른 글
| [URECA] Day22 | 알고리즘 | 그래프 응용(백트래킹, 위상 정렬) (0) | 2025.02.25 |
|---|---|
| [URECA] Day21 | 알고리즘 | MST 알고리즘 (1) | 2025.02.24 |
| [URECA] Day 19 | 알고리즘 | 그래프 (0) | 2025.02.20 |
| [URECA] Day 18 | 알고리즘 | 비선형 자료구조 (0) | 2025.02.19 |
| [URECA] Day17 | 알고리즘 | 순두부가 아닌 순(열) 조(합) 부(분집합) (0) | 2025.02.18 |
728x90
그래프를 탐색하는 방법 2 - BFS(Breadth-First Search) : 인접행렬-O(V^2), 인접리스트- O(V + E)

BFS_인접행렬 코드
/*
https://www.acmicpc.net/problem/1260
4 5 1
1 2
1 3
1 4
2 4
3 4
*/
package ureca;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class BFS_인접행렬{
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
StringBuilder sb = new StringBuilder(100);
//입력 받음
int V=scanner.nextInt(); // 정점의 개수
int E=scanner.nextInt(); // 간선의 개수
int startNo = scanner.nextInt(); // 탐색 시작할 정점 번호
int[][] adjMatrix = new int[V + 1][V + 1]; // 간선 정보를 넣을 배열, 시작정점이 1이라면 0번행열은 쓰지 않는게 좋음
boolean []isSelected=new boolean[V+1];
// 간선 정보를 입력받아 인접 행렬을 구성
for (int i = 0; i < E; i++) {
int from = scanner.nextInt();
int to = scanner.nextInt();
adjMatrix[from][to] = adjMatrix[to][from] = 1; // 무방향 그래프이므로
}
// BFS 탐색 시작
Queue<Integer> queue = new LinkedList<>(); // 큐 생성
queue.offer(startNo); // 시작 정점 큐에 추가
isSelected[startNo] = true; // 시작 정점 방문 처리
while (!queue.isEmpty()) {
int cur = queue.poll(); // 큐에서 정점 꺼내기
sb.append(cur).append(" "); // 결과 문자열에 추가
// 현재 정점에서 갈 수 있는 모든 후보지 탐색
for (int i = 1; i <= V; i++) {
if (!isSelected[i] && adjMatrix[cur][i] != 0) { // 방문하지 않았고, 연결된 정점인 경우
queue.offer(i); // 큐에 추가
isSelected[i] = true; // 방문 처리
}
}
}
sb.append("\n");
// 결과 출력
System.out.print(sb.toString());
scanner.close();
}
}BFS_인접리스트 코드
import java.util.*;
public class 백준_1260_BFS_인접리스트 {
static List<List<Integer>> list=new ArrayList();
static boolean[] isSelected;
static StringBuilder sb=new StringBuilder();
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
isSelected=new boolean[n+1];
for (int i = 1; i <= n+1; i++) {
list.add(new ArrayList());
}
int m=sc.nextInt();
int startNode=sc.nextInt();
for(int i=0;i<m;i++) {
int u=sc.nextInt();
int v=sc.nextInt();
list.get(u).add(v);
list.get(v).add(u);
}
Queue<Integer> q=new LinkedList();
q.offer(startNode);
isSelected[startNode]=true;
while(!q.isEmpty()) {
int curNode=q.poll();
sb.append(curNode).append(" ");
for (int i :list.get(curNode)) {
if(!isSelected[i]) {
q.offer(i);
isSelected[i]=true;
}
}
}
System.out.println(sb);
}
}(6) 그래프 응용 - 최단경로
a)가중치가 없는 그래프에서 정점간의 최단 경로를 찾는 방법은 BFS가 최고 (ex. 바둑판 미로 찾기)
i)경로를 추적하기 위해 parent의 정보를 저장할 배열을 사용하는 경우
/*
### 문제: 최단 경로 찾기
**문제 설명**
주어진 무방향 그래프에서 두 노드 간의 최단 경로를 찾는 프로그램을 작성하시오. 그래프는 N개의 노드와 M개의 간선으로 구성되어 있으며, 각 간선은 두 노드를 연결합니다. 시작 노드와 목표 노드가 주어질 때, 이 두 노드 간의 최단 경로를 출력하시오.
**입력**
- 첫째 줄에 두 개의 정수 N(1 ≤ N ≤ 1000)과 M(1 ≤ M ≤ 10000)이 주어진다. N은 노드의 개수, M은 간선의 개수이다.
- 다음 M개의 줄에는 간선 정보가 주어진다. 각 줄은 두 개의 정수 u와 v(1 ≤ u, v ≤ N)를 포함하며, 이는 노드 u와 노드 v가 간선으로 연결되어 있음을 의미한다.
- 마지막 줄에는 시작 노드 S와 목표 노드 G가 주어진다.
**출력**
- 시작 노드 S에서 목표 노드 G까지의 최단 경로를 출력한다. 경로는 노드 번호로 구성되어야 하며, 경로가 존재하지 않는 경우 `-1`을 출력한다.
**입력**
5 5
1 2
1 3
2 4
3 4
4 5
1 5
**출력**
1 2 4 5
*/
import java.util.*;
public class BFS_최단경로 {
static StringBuilder sb = new StringBuilder(); // 경로를 저장할 StringBuilder
static List<Integer> path = new ArrayList<>(); // 최단 경로를 저장할 리스트
static boolean found = false; // 경로가 발견되었는지 여부를 저장하는 변수
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 노드의 수 N과 간선의 수 M을 입력받음
int N = sc.nextInt(); // 노드의 수
int M = sc.nextInt(); // 간선의 수
// 인접 리스트를 생성
List<List<Integer>> list = new ArrayList<>();
for (int i = 0; i <= N; i++) {
list.add(new ArrayList<>()); // 각 노드에 대한 리스트 초기화
}
// 간선 정보를 입력받아 인접 리스트에 추가
for (int i = 0; i < M; i++) {
int from = sc.nextInt(); // 간선의 시작 노드
int to = sc.nextInt(); // 간선의 끝 노드
list.get(from).add(to); // 양방향 그래프이므로 양쪽에 추가
list.get(to).add(from);
}
// 시작 노드 S와 목표 노드 G를 입력받음
int start = sc.nextInt();
int goal = sc.nextInt();
// 방문 여부를 체크할 배열
boolean[] visited = new boolean[N + 1];
// 부모 노드를 저장할 배열 (경로 추적을 위해 사용)
int[] parent = new int[N + 1];
// BFS를 위한 큐 초기화
Queue<Integer> q = new LinkedList<>();
q.offer(start); // 시작 노드를 큐에 추가
visited[start] = true; // 시작 노드를 방문 처리
parent[start] = -1; // 시작 노드의 부모는 없음
// BFS 탐색 시작
while (!q.isEmpty()) {
int cur = q.poll(); // 큐에서 현재 노드를 꺼냄
// 목표 노드에 도달한 경우
if (cur == goal) {
found = true; // 경로 발견
break; // 탐색 종료
}
// 현재 노드와 연결된 모든 노드를 탐색
for (int i : list.get(cur)) {
if (!visited[i]) { // 방문하지 않은 노드인 경우
q.offer(i); // 큐에 추가
visited[i] = true; // 방문 처리
parent[i] = cur; // 현재 노드를 부모로 설정
}
}
}
if (found) {// 경로가 발견된 경우
// 목표 노드에서 시작 노드까지 부모를 통해 경로를 추적
for (int at = goal; at != -1; at = parent[at]) {
sb.append(at).append(" "); // 결과에 추가
}
System.out.println(sb.reverse().toString().trim());
}else{
System.out.println(-1);
}
}
}728x90
'💡 URECA > 🗒️ 스터디 노트' 카테고리의 다른 글
| [URECA] Day22 | 알고리즘 | 그래프 응용(백트래킹, 위상 정렬) (0) | 2025.02.25 |
|---|---|
| [URECA] Day21 | 알고리즘 | MST 알고리즘 (1) | 2025.02.24 |
| [URECA] Day 19 | 알고리즘 | 그래프 (0) | 2025.02.20 |
| [URECA] Day 18 | 알고리즘 | 비선형 자료구조 (0) | 2025.02.19 |
| [URECA] Day17 | 알고리즘 | 순두부가 아닌 순(열) 조(합) 부(분집합) (0) | 2025.02.18 |

