MST 알고리즘
Kruskal(대표적인 그리디 알고리즘)
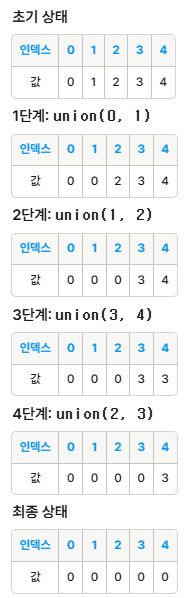
서로소 집합
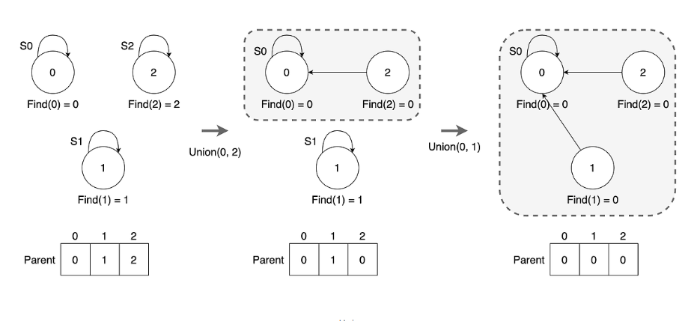
서로소 집합 코드
public class DisjointSetExample {
// 부모 노드를 저장할 배열
static int[] p;
// 집합을 초기화하는 메서드
static void makeSet(int V) {
// V개의 원소를 가지는 배열을 생성
p = new int[V];
// 각 원소의 부모를 자기 자신으로 초기화
for (int i = 0; i < V; i++) {
p[i] = i;
}
}
// 두 원소를 결합하는 메서드
static boolean union(int f, int t) {
// 각 원소의 루트 부모를 찾음
int fp = find(f);
int tp = find(t);
// 이미 같은 집합에 속하는 경우, 결합할 필요 없음
if (fp == tp) return false;
// 두 집합을 결합: t의 부모를 f의 부모로 설정
p[tp] = fp;
return true; // 결합 성공
}
// 원소의 루트 부모를 찾는 메서드
static int find(int e) {
// 경로 압축을 통해 트리의 높이를 줄임
if (e != p[e]) {
p[e] = find(p[e]); // 재귀적으로 부모를 찾음
}
return p[e]; // 최종 부모 반환
}
public static void main(String[] args) {
// 5개의 원소(0, 1, 2, 3, 4)로 집합을 초기화
makeSet(5);
// 원소 0과 1을 결합
union(0, 1);
// 원소 1과 2를 결합
union(1, 2);
// 원소 3과 4를 결합
union(3, 4);
// 원소 0의 루트 부모를 찾음 (0, 1, 2는 같은 집합)
System.out.println("Root of 0: " + find(0)); // 출력: Root of 0: 0
// 원소 1의 루트 부모를 찾음
System.out.println("Root of 1: " + find(1)); // 출력: Root of 1: 0
// 원소 2의 루트 부모를 찾음
System.out.println("Root of 2: " + find(2)); // 출력: Root of 2: 0
// 원소 3의 루트 부모를 찾음
System.out.println("Root of 3: " + find(3)); // 출력: Root of 3: 3
// 원소 4의 루트 부모를 찾음
System.out.println("Root of 4: " + find(4)); // 출력: Root of 4: 3
// 원소 0과 3의 루트 부모를 비교하여 서로 다른 집합인지 확인
System.out.println("Are 0 and 3 in the same set? " + (find(0) == find(3))); // 출력: false
// 원소 2와 3을 결합
union(2, 3);
// 결합 후 다시 루트 부모를 확인
System.out.println("Root of 3 after union with 2: " + find(3)); // 출력: Root of 3: 0
System.out.println("Are 0 and 3 in the same set now? " + (find(0) == find(3))); // 출력: true
}
}Kruskal 설명 (O(E log V))
이전 단계에서 만들어진 신장 트리와는 상관없이 무조건 최소 간선만을 선택하는 방법
방법:
1. 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
2. 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다.
* 즉, 가장 낮은 가중치를 먼저 선택한다.
* 사이클을 형성하는 간선을 제외한다.(==>union()이 false이면 이미 같은 집합이므로 사이클이 있다고 간주함)
3. 해당 간선을 현재의 MST(최소 비용 신장 트리)의 집합에 추가한다.
4. 위(2~3)의 과정을 트리가 (V-1)개의 간선을 가질 때까지 반복한다.
Kruskal 코드
/*
Q. 모든 정점을 연결하는 최소 비용을 구하라(ex.모든 도시를 여행하는 최소 비용을 구하라)
첫째줄:정점 개수
둘째줄:간선 개수
나머지:간선 정보
7
11
0 1 32
0 2 31
0 5 60
0 6 51
1 2 21
2 4 46
2 6 25
3 4 34
3 5 18
4 5 40
4 6 51
*/
// 엑셀 그림 참조
package jes;
import java.io.*;
import java.util.Arrays;
public class A076_크루스칼 {
public static void main(String[] args) throws Exception{
//System.setIn(new FileInputStream("src/jes/크루스칼.txt"));
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw=new BufferedWriter(new OutputStreamWriter(System.out));
StringBuilder sb=new StringBuilder(100);
int V=Integer.parseInt(br.readLine().trim());
int E=Integer.parseInt(br.readLine().trim());
Edge []arr=new Edge[E];
for (int i = 0; i < E; i++) {
String []ftw=br.readLine().split(" ");
int from=Integer.parseInt(ftw[0]);
int to=Integer.parseInt(ftw[1]);
int weight=Integer.parseInt(ftw[2]);
arr[i]=new Edge(from, to, weight); //(2)
}
Arrays.sort(arr);// (3)
makeSet(V); // (4)
int result=0; //(5)
int pickCnt=0; //(6)
for(Edge e:arr) { //(7)
if(union(e.f,e.t)) {
result+=e.w;
if(++pickCnt==(V-1))break;
}
}
sb.append(result);
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
static boolean union(int f,int t) {
int fp=find(f);
int tp=find(t);
if(fp==tp) return false;
p[tp]=fp;
return true;
}
static int find(int e) {
if(e!=p[e]) p[e]=find(p[e]);
return p[e];
}
static int[]p;
static void makeSet(int V) {
p=new int[V];
for (int i = 0; i < V; i++) {
p[i]=i;
}
}
static class Edge implements Comparable<Edge>{ //(1)
int f,t,w;
public Edge(int f, int t, int w) {
super();
this.f = f;
this.t = t;
this.w = w;
}
@Override
public String toString() {
return "Edge [f=" + f + ", t=" + t + ", w=" + w + "]";
}
@Override
public int compareTo(Edge o) {
// TODO Auto-generated method stub
return Integer.compare(w, o.w);
}
}
}
Prim (대표적인 그리디 알고리즘)
Prim 설명
간선이 많으면 크루스칼에서는 정렬에 시간이 많이 든다. 이럴때는 정점 기반 처리를 하는 프림을 쓴다.
(간적쿠간만프)
ex) 최대간선 = V *(V–1)/ 2
만약 정점이 1만일때 최대 간선 수는 5천만쯤 되니, 주어진 간선 수가 2500 이하이면 Kruskal을, 그 이상이면 Prim을 쓴다.
방법:
1. 시작 단계에서는 시작 정점만이 MST(최소 비용 신장 트리) 집합에 포함된다.
2. 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선(PriorityQueue이용하면 쉬움)으로 연결된 정점을 선택하여 트리를 확장한다.즉, 가장 낮은 가중치를 먼저 선택한다.
3. 모든 정점이 선택되었으면 끝냄.
/*
Q. 모든 정점을 연결하는 최소 비용을 구하라(ex.모든 도시를 여행하는 최소 비용을 구하라)
첫째줄:정점 개수
둘째줄:간선 개수
나머지:간선 정보
7
11
0 1 32
0 2 31
0 5 60
0 6 51
1 2 21
2 4 46
2 6 25
3 4 34
3 5 18
4 5 40
4 6 51
*/
// 엑셀 그림 참조
package jes;
import java.io.*;
import java.util.PriorityQueue;
public class Prim {
public static void main(String[] args) throws Exception{
//System.setIn(new FileInputStream("src/jes/프림.txt"));
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw=new BufferedWriter(new OutputStreamWriter(System.out));
StringBuilder sb=new StringBuilder(100);
int V=Integer.parseInt(br.readLine().trim());
int E=Integer.parseInt(br.readLine().trim());
int [][]arr=new int[V][V]; //(1)
for (int i = 0; i < E; i++) {
String []ftw=br.readLine().split(" ");
int from=Integer.parseInt(ftw[0]);
int to=Integer.parseInt(ftw[1]);
int weight=Integer.parseInt(ftw[2]);
arr[from][to]=arr[to][from]=weight;
}
boolean []visited=new boolean[V];//(2)
int result=0;//(3)
int pickCnt=0;//(4)
PriorityQueue<Edge> pq=new PriorityQueue<>();//(5)
//처리
pq.offer(new Edge(0,0,0)); //1
while(!pq.isEmpty()) {//2
Edge e=pq.poll();//2-1
if(visited[e.t]) continue;//2-2
visited[e.t]=true;//2-3
result+=e.w;//2-4
if(++pickCnt==V) break;//2-5
for (int nt = 0; nt < V; nt++) {//2-6
if(!visited[nt] && arr[e.t][nt]!=0 ) pq.offer(new Edge(e.t,nt,arr[e.t][nt]));//2-6-1
}
}
sb.append(result);
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
static class Edge implements Comparable<Edge>{ //(6)
int f,t,w;
public Edge(int f, int t, int w) {
super();
this.f = f;
this.t = t;
this.w = w;
}
@Override
public String toString() {
return "Edge [f=" + f + ", t=" + t + ", w=" + w + "]";
}
@Override
public int compareTo(Edge o) {
// TODO Auto-generated method stub
return Integer.compare(w, o.w);
}
}
}
조별 스터디 문제
문제 1: 최소 비용 도로 건설 문제 설명 어떤 나라에는 N개의 도시가 있고, 일부 도시들은 도로로 연결되어 있다. 정부는 모든 도시를 최 소한의 비용으로 연결하려 한다. 각 도로는 두 도시를 연결하며 특정 비용이 든다. 모든 도시를 연결하는 최소 비용을 구하시오.
입력
첫 번째 줄에 도시의 개수 N과 도로의 개수 M이 주어진다. 다음 M개의 줄에는 u,v,k 가 주어지며, 이는 도시 u와 도시 v를 연결하는 도로의 비용이 k임을 의미한다. 출력 모든 도시를 연결하는 최소 비용을 출력하시오.
제한
1≤N≤10^5
1≤M≤2×10^5
1≤k≤10^6
예시 입력 :
4 5
1 2 1
1 3 2
1 4 3
2 3 1
3 4 1
출력 : 3
import java.util.*;
import java.io.*;
public class Main {
static class Edge implements Comparable<Edge> {
int u, v, w;
Edge(int u, int v, int w) { this.u = u; this.v = v; this.w = w; }
public int compareTo(Edge other) { return this.w - other.w; }
}
static int[] parent;
static int find(int x) {
if(parent[x] == x) return x;
return parent[x] = find(parent[x]);
}
static void union(int a, int b) {
int pa = find(a), pb = find(b);
if(pa != pb) parent[pb] = pa;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
Edge[] edges = new Edge[m];
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
edges[i] = new Edge(u, v, w);
}
Arrays.sort(edges);
parent = new int[n + 1];
for (int i = 1; i <= n; i++) parent[i] = i;
long cost = 0;
int cnt = 0;
for (Edge e : edges) {
if (find(e.u) != find(e.v)) {
union(e.u, e.v);
cost += e.w;
cnt++;
if (cnt == n - 1) break;
}
}
System.out.println(cost);
}
}
문제 2:
전력망 복구 문제 설명 어떤 나라에는 N개의 발전소와 전력망이 있으며, 일부 발전소는 전력을 공급하기 위해 전력망을 통해 다른 발전소와 연결되어 있다. 자연 재해로 일부 전력망이 파손되어 복구가 필요하다. 정부 는 최소한의 비용으로 전력망을 복구하여 모든 발전소가 전력을 공급받을 수 있도록 해야 한다. 각 전력망의 복구 비용이 다르고, 두 발전소를 연결할 수 있는 여러 가지 전력망이 존재한다. 최 소 비용으로 전력망을 복구하는 방법을 구하시오.
입력
첫 번째 줄에 발전소의 개수 N과 전력망의 개수 M이 주어진다. 다음 M개의 줄에는 u,v,k가 주어지며, 이는 발전소 u와 발전소 v를 연결하는 전력망의 복구 비용 이 k임을 의미한다. 출력 모든 발전소를 연결하는 최소 비용을 출력하시오.
제한
2≤N≤10^5
1≤M≤2×10^5
1≤w≤10^6
예시 입력 :
5 6
1 2 3
1 3 4
2 3 1
2 4 2
3 4 5
4 5 6
출력 : 10
import java.util.*;
import java.io.*;
public class Main {
static class Edge implements Comparable<Edge> {
int u, v, cost;
Edge(int u, int v, int cost) {
this.u = u;
this.v = v;
this.cost = cost;
}
public int compareTo(Edge other) {
return this.cost - other.cost;
}
}
static int[] parent;
static int find(int x) {
if (parent[x] == x) return x;
return parent[x] = find(parent[x]);
}
static void union(int a, int b) {
int pa = find(a);
int pb = find(b);
if (pa != pb) parent[pb] = pa;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
Edge[] edges = new Edge[m];
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
edges[i] = new Edge(u, v, cost);
}
Arrays.sort(edges);
parent = new int[n + 1];
for (int i = 1; i <= n; i++) parent[i] = i;
long totalCost = 0;
int count = 0;
for (Edge e : edges) {
if (find(e.u) != find(e.v)) {
union(e.u, e.v);
totalCost += e.cost;
count++;
if (count == n - 1) break;
}
}
System.out.println(totalCost);
}
}'💡 URECA > 🗒️ 스터디 노트' 카테고리의 다른 글
| [URECA] Day 23 | Git (0) | 2025.02.26 |
|---|---|
| [URECA] Day22 | 알고리즘 | 그래프 응용(백트래킹, 위상 정렬) (0) | 2025.02.25 |
| [URECA] Day 20 | 알고리즘 | 그래프 (2) (1) | 2025.02.21 |
| [URECA] Day 19 | 알고리즘 | 그래프 (0) | 2025.02.20 |
| [URECA] Day 18 | 알고리즘 | 비선형 자료구조 (0) | 2025.02.19 |
MST 알고리즘
Kruskal(대표적인 그리디 알고리즘)
서로소 집합

서로소 집합 코드

public class DisjointSetExample {
// 부모 노드를 저장할 배열
static int[] p;
// 집합을 초기화하는 메서드
static void makeSet(int V) {
// V개의 원소를 가지는 배열을 생성
p = new int[V];
// 각 원소의 부모를 자기 자신으로 초기화
for (int i = 0; i < V; i++) {
p[i] = i;
}
}
// 두 원소를 결합하는 메서드
static boolean union(int f, int t) {
// 각 원소의 루트 부모를 찾음
int fp = find(f);
int tp = find(t);
// 이미 같은 집합에 속하는 경우, 결합할 필요 없음
if (fp == tp) return false;
// 두 집합을 결합: t의 부모를 f의 부모로 설정
p[tp] = fp;
return true; // 결합 성공
}
// 원소의 루트 부모를 찾는 메서드
static int find(int e) {
// 경로 압축을 통해 트리의 높이를 줄임
if (e != p[e]) {
p[e] = find(p[e]); // 재귀적으로 부모를 찾음
}
return p[e]; // 최종 부모 반환
}
public static void main(String[] args) {
// 5개의 원소(0, 1, 2, 3, 4)로 집합을 초기화
makeSet(5);
// 원소 0과 1을 결합
union(0, 1);
// 원소 1과 2를 결합
union(1, 2);
// 원소 3과 4를 결합
union(3, 4);
// 원소 0의 루트 부모를 찾음 (0, 1, 2는 같은 집합)
System.out.println("Root of 0: " + find(0)); // 출력: Root of 0: 0
// 원소 1의 루트 부모를 찾음
System.out.println("Root of 1: " + find(1)); // 출력: Root of 1: 0
// 원소 2의 루트 부모를 찾음
System.out.println("Root of 2: " + find(2)); // 출력: Root of 2: 0
// 원소 3의 루트 부모를 찾음
System.out.println("Root of 3: " + find(3)); // 출력: Root of 3: 3
// 원소 4의 루트 부모를 찾음
System.out.println("Root of 4: " + find(4)); // 출력: Root of 4: 3
// 원소 0과 3의 루트 부모를 비교하여 서로 다른 집합인지 확인
System.out.println("Are 0 and 3 in the same set? " + (find(0) == find(3))); // 출력: false
// 원소 2와 3을 결합
union(2, 3);
// 결합 후 다시 루트 부모를 확인
System.out.println("Root of 3 after union with 2: " + find(3)); // 출력: Root of 3: 0
System.out.println("Are 0 and 3 in the same set now? " + (find(0) == find(3))); // 출력: true
}
}Kruskal 설명 (O(E log V))
이전 단계에서 만들어진 신장 트리와는 상관없이 무조건 최소 간선만을 선택하는 방법
방법:
1. 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
2. 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다.
* 즉, 가장 낮은 가중치를 먼저 선택한다.
* 사이클을 형성하는 간선을 제외한다.(==>union()이 false이면 이미 같은 집합이므로 사이클이 있다고 간주함)
3. 해당 간선을 현재의 MST(최소 비용 신장 트리)의 집합에 추가한다.
4. 위(2~3)의 과정을 트리가 (V-1)개의 간선을 가질 때까지 반복한다.
Kruskal 코드
/*
Q. 모든 정점을 연결하는 최소 비용을 구하라(ex.모든 도시를 여행하는 최소 비용을 구하라)
첫째줄:정점 개수
둘째줄:간선 개수
나머지:간선 정보
7
11
0 1 32
0 2 31
0 5 60
0 6 51
1 2 21
2 4 46
2 6 25
3 4 34
3 5 18
4 5 40
4 6 51
*/
// 엑셀 그림 참조
package jes;
import java.io.*;
import java.util.Arrays;
public class A076_크루스칼 {
public static void main(String[] args) throws Exception{
//System.setIn(new FileInputStream("src/jes/크루스칼.txt"));
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw=new BufferedWriter(new OutputStreamWriter(System.out));
StringBuilder sb=new StringBuilder(100);
int V=Integer.parseInt(br.readLine().trim());
int E=Integer.parseInt(br.readLine().trim());
Edge []arr=new Edge[E];
for (int i = 0; i < E; i++) {
String []ftw=br.readLine().split(" ");
int from=Integer.parseInt(ftw[0]);
int to=Integer.parseInt(ftw[1]);
int weight=Integer.parseInt(ftw[2]);
arr[i]=new Edge(from, to, weight); //(2)
}
Arrays.sort(arr);// (3)
makeSet(V); // (4)
int result=0; //(5)
int pickCnt=0; //(6)
for(Edge e:arr) { //(7)
if(union(e.f,e.t)) {
result+=e.w;
if(++pickCnt==(V-1))break;
}
}
sb.append(result);
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
static boolean union(int f,int t) {
int fp=find(f);
int tp=find(t);
if(fp==tp) return false;
p[tp]=fp;
return true;
}
static int find(int e) {
if(e!=p[e]) p[e]=find(p[e]);
return p[e];
}
static int[]p;
static void makeSet(int V) {
p=new int[V];
for (int i = 0; i < V; i++) {
p[i]=i;
}
}
static class Edge implements Comparable<Edge>{ //(1)
int f,t,w;
public Edge(int f, int t, int w) {
super();
this.f = f;
this.t = t;
this.w = w;
}
@Override
public String toString() {
return "Edge [f=" + f + ", t=" + t + ", w=" + w + "]";
}
@Override
public int compareTo(Edge o) {
// TODO Auto-generated method stub
return Integer.compare(w, o.w);
}
}
}
Prim (대표적인 그리디 알고리즘)
Prim 설명
간선이 많으면 크루스칼에서는 정렬에 시간이 많이 든다. 이럴때는 정점 기반 처리를 하는 프림을 쓴다.
(간적쿠간만프)
ex) 최대간선 = V *(V–1)/ 2
만약 정점이 1만일때 최대 간선 수는 5천만쯤 되니, 주어진 간선 수가 2500 이하이면 Kruskal을, 그 이상이면 Prim을 쓴다.
방법:
1. 시작 단계에서는 시작 정점만이 MST(최소 비용 신장 트리) 집합에 포함된다.
2. 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선(PriorityQueue이용하면 쉬움)으로 연결된 정점을 선택하여 트리를 확장한다.즉, 가장 낮은 가중치를 먼저 선택한다.
3. 모든 정점이 선택되었으면 끝냄.
/*
Q. 모든 정점을 연결하는 최소 비용을 구하라(ex.모든 도시를 여행하는 최소 비용을 구하라)
첫째줄:정점 개수
둘째줄:간선 개수
나머지:간선 정보
7
11
0 1 32
0 2 31
0 5 60
0 6 51
1 2 21
2 4 46
2 6 25
3 4 34
3 5 18
4 5 40
4 6 51
*/
// 엑셀 그림 참조
package jes;
import java.io.*;
import java.util.PriorityQueue;
public class Prim {
public static void main(String[] args) throws Exception{
//System.setIn(new FileInputStream("src/jes/프림.txt"));
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw=new BufferedWriter(new OutputStreamWriter(System.out));
StringBuilder sb=new StringBuilder(100);
int V=Integer.parseInt(br.readLine().trim());
int E=Integer.parseInt(br.readLine().trim());
int [][]arr=new int[V][V]; //(1)
for (int i = 0; i < E; i++) {
String []ftw=br.readLine().split(" ");
int from=Integer.parseInt(ftw[0]);
int to=Integer.parseInt(ftw[1]);
int weight=Integer.parseInt(ftw[2]);
arr[from][to]=arr[to][from]=weight;
}
boolean []visited=new boolean[V];//(2)
int result=0;//(3)
int pickCnt=0;//(4)
PriorityQueue<Edge> pq=new PriorityQueue<>();//(5)
//처리
pq.offer(new Edge(0,0,0)); //1
while(!pq.isEmpty()) {//2
Edge e=pq.poll();//2-1
if(visited[e.t]) continue;//2-2
visited[e.t]=true;//2-3
result+=e.w;//2-4
if(++pickCnt==V) break;//2-5
for (int nt = 0; nt < V; nt++) {//2-6
if(!visited[nt] && arr[e.t][nt]!=0 ) pq.offer(new Edge(e.t,nt,arr[e.t][nt]));//2-6-1
}
}
sb.append(result);
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
static class Edge implements Comparable<Edge>{ //(6)
int f,t,w;
public Edge(int f, int t, int w) {
super();
this.f = f;
this.t = t;
this.w = w;
}
@Override
public String toString() {
return "Edge [f=" + f + ", t=" + t + ", w=" + w + "]";
}
@Override
public int compareTo(Edge o) {
// TODO Auto-generated method stub
return Integer.compare(w, o.w);
}
}
}
조별 스터디 문제
문제 1: 최소 비용 도로 건설 문제 설명 어떤 나라에는 N개의 도시가 있고, 일부 도시들은 도로로 연결되어 있다. 정부는 모든 도시를 최 소한의 비용으로 연결하려 한다. 각 도로는 두 도시를 연결하며 특정 비용이 든다. 모든 도시를 연결하는 최소 비용을 구하시오.
입력
첫 번째 줄에 도시의 개수 N과 도로의 개수 M이 주어진다. 다음 M개의 줄에는 u,v,k 가 주어지며, 이는 도시 u와 도시 v를 연결하는 도로의 비용이 k임을 의미한다. 출력 모든 도시를 연결하는 최소 비용을 출력하시오.
제한
1≤N≤10^5
1≤M≤2×10^5
1≤k≤10^6
예시 입력 :
4 5
1 2 1
1 3 2
1 4 3
2 3 1
3 4 1
출력 : 3
import java.util.*;
import java.io.*;
public class Main {
static class Edge implements Comparable<Edge> {
int u, v, w;
Edge(int u, int v, int w) { this.u = u; this.v = v; this.w = w; }
public int compareTo(Edge other) { return this.w - other.w; }
}
static int[] parent;
static int find(int x) {
if(parent[x] == x) return x;
return parent[x] = find(parent[x]);
}
static void union(int a, int b) {
int pa = find(a), pb = find(b);
if(pa != pb) parent[pb] = pa;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
Edge[] edges = new Edge[m];
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
edges[i] = new Edge(u, v, w);
}
Arrays.sort(edges);
parent = new int[n + 1];
for (int i = 1; i <= n; i++) parent[i] = i;
long cost = 0;
int cnt = 0;
for (Edge e : edges) {
if (find(e.u) != find(e.v)) {
union(e.u, e.v);
cost += e.w;
cnt++;
if (cnt == n - 1) break;
}
}
System.out.println(cost);
}
}
문제 2:
전력망 복구 문제 설명 어떤 나라에는 N개의 발전소와 전력망이 있으며, 일부 발전소는 전력을 공급하기 위해 전력망을 통해 다른 발전소와 연결되어 있다. 자연 재해로 일부 전력망이 파손되어 복구가 필요하다. 정부 는 최소한의 비용으로 전력망을 복구하여 모든 발전소가 전력을 공급받을 수 있도록 해야 한다. 각 전력망의 복구 비용이 다르고, 두 발전소를 연결할 수 있는 여러 가지 전력망이 존재한다. 최 소 비용으로 전력망을 복구하는 방법을 구하시오.
입력
첫 번째 줄에 발전소의 개수 N과 전력망의 개수 M이 주어진다. 다음 M개의 줄에는 u,v,k가 주어지며, 이는 발전소 u와 발전소 v를 연결하는 전력망의 복구 비용 이 k임을 의미한다. 출력 모든 발전소를 연결하는 최소 비용을 출력하시오.
제한
2≤N≤10^5
1≤M≤2×10^5
1≤w≤10^6
예시 입력 :
5 6
1 2 3
1 3 4
2 3 1
2 4 2
3 4 5
4 5 6
출력 : 10
import java.util.*;
import java.io.*;
public class Main {
static class Edge implements Comparable<Edge> {
int u, v, cost;
Edge(int u, int v, int cost) {
this.u = u;
this.v = v;
this.cost = cost;
}
public int compareTo(Edge other) {
return this.cost - other.cost;
}
}
static int[] parent;
static int find(int x) {
if (parent[x] == x) return x;
return parent[x] = find(parent[x]);
}
static void union(int a, int b) {
int pa = find(a);
int pb = find(b);
if (pa != pb) parent[pb] = pa;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
Edge[] edges = new Edge[m];
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
edges[i] = new Edge(u, v, cost);
}
Arrays.sort(edges);
parent = new int[n + 1];
for (int i = 1; i <= n; i++) parent[i] = i;
long totalCost = 0;
int count = 0;
for (Edge e : edges) {
if (find(e.u) != find(e.v)) {
union(e.u, e.v);
totalCost += e.cost;
count++;
if (count == n - 1) break;
}
}
System.out.println(totalCost);
}
}'💡 URECA > 🗒️ 스터디 노트' 카테고리의 다른 글
| [URECA] Day 23 | Git (0) | 2025.02.26 |
|---|---|
| [URECA] Day22 | 알고리즘 | 그래프 응용(백트래킹, 위상 정렬) (0) | 2025.02.25 |
| [URECA] Day 20 | 알고리즘 | 그래프 (2) (1) | 2025.02.21 |
| [URECA] Day 19 | 알고리즘 | 그래프 (0) | 2025.02.20 |
| [URECA] Day 18 | 알고리즘 | 비선형 자료구조 (0) | 2025.02.19 |

